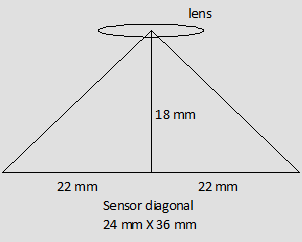
[All of the below is in reference to rectangular-perspective lenses without lens distortion.] Most people, if asked, "If you have two lenses that fit the same camera, and one has 1/2 the focal length of the other, is that lens twice as wide as the other?", would answer, "Yes.", but 'tain't necessarily so...;-) If we assume a 24mm x 36mm frame size (which it is for 35mm film or for a full-frame digital sensor), the frame diagonal (which is used for finding the angle of coverage of a particular lens for the format diagonal) is 24mm squared (576) plus 36mm squared (1296) added together (to get 1872) - and the square root of this is 43.27mm. Let's call it 44mm to simplify calculating, since it is very close to the real format "normal" focal length for 35mm film cameras. Two identical right triangles can be made by drawing a vertical line perpendicular to the frame diagonal line and intersecting it in its center (to represent a non-shifted lens of a given focal length) in order to find 1/2 the angle of coverage of a lens with this format using trigonometry, with the length of that new line being equal to the lens focal length. Lines are then drawn connecting the free end of the vertical line with the free ends of the line representing the sensor diagonal (representing the total angle of coverage of the lens, now made up of the two right triangles). For an 18mm lens example, that gives 18mm for the vertical line side of the triangles, and horizontal line sides of the triangles of 1/2 of 44mm, or 22mm (in order to solve for 1/2 the total angle of view of the lens using right triangles). See drawing below -- One now has everything needed except a calculator that
provides angles when trigonometric "tangent" values of the angles are
entered. In a right triangle, the opposite side of the triangle from the
angle, divided by the side adjacent to it (but not the diagonal line of
the triangle,
or "hypotenuse"), gives the tangent for the angle in degrees between the vertical line and the
hypotenuse, or 22/18 = 1.22. The angle for that tangent value is 50.66 degrees, which is
one half of the full angle for the format diagonal (which was split in two to solve for the angle in Continuing
(with lens angles of view with doubled/halved focal lengths on a
35mm-size frame, as
calculated using the format diagonal, with results rounded to two decimal places,
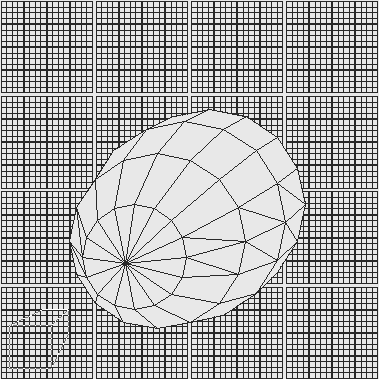
and with the coverage ratios given), here are the results -- It also follows from this that as the focal lengths are shortened toward the wide angle end, the image magnifications on the sensor (generally negative compared with the subject in cameras) do not follow the simple arithmetic proportional changes of the focal lengths. Further complicating this is the need for more information on how particular lenses focus unless all the lenses of interest are focused correctly at a given distance, all are truly properly rated for focal length at that distance (not commonly true), and all focus in the same way (if focused away from infinity). The last can cause results to vary considerably, since simple lenses cause a narrowing of angle of view with closer focus, but internal-focus lenses and zooms can go wider or narrower with closer focus. OK, now if one asks, "Do things get wider toward the edges in the images made by super wide lenses?", the answer is generally, "Yes!" - but, again, t'ain't necessarily so (but this time, it is more likely to be so sometimes...;-). If a large grid of equally-sized squares is photographed (let's assume 24 squares in one direction, 36 in the other, on a plane parallel with the same film or sensor size as used above, with the grid just filling the image area) with two lenses, one a super-wide, and the other of much longer focal length, the resulting images would look the same. Even if each square has a circle drawn inside it, the resulting images would still look the same. OK, I can hear the chorus of sputterings of, "But, but, but!"s, now - and here are a couple of photos of mine that may support that skepticism: We are all familiar with the "egghead" look of people's heads appearing near the corners of images taken with super-wides. But, neither if these lenses (a 12mm Voightlander and a 15mm Nikkor) "distorts" noticeably, since both follow very closely the requirements for low linear distortion within their perspective type (see www.David-Ruether-Photography.com/lens_perspective_types.htm, www.David-Ruether-Photography.com/lens_distortion_types.htm, www.David-Ruether-Photography.com/seeing_and_perspective.htm for more). It is the 3D nature of the subjects and varying distances from the lenses that cause the "upset", not distortion. (BTW, I include the other perspective types as also being distortion free so long as their imaging characteristics are properly followed - and they are also capable of being used to make fine images...) Back to concepts: if that frame-filling grid of 24 x 36 squares has a hemisphere placed inside each square, flat side down, and the resulting form is photographed straight-on with a very long lens, the result will be similar to the images made with the circles in the squares. If the same thing is done with a super-wide lens, the changed points of view relative to the hemispheres (with the lens moved closer in to fill the image frame with the squares) will cause them to look elongated outward from the image center, the more so the farther they are from the center (due to the changing angles of view of them from the close in viewpoint) - but, there is still no distortion! ;-) Thanks to Dave Martindale for pointing out an error in my original article, and to Paul Furman for the use of this drawing illustrating what a hemisphere would look like toward the corner of the field of view of a very wide angle lens - and that cross sections of the hemisphere taken parallel with the sensor remain circular --
|